Matlab toolbox demos

The Toast-Matlab toolbox contains a series of interactive demos that allow to explore specific topics of the forward and inverse problems in diffuse optical tomography. Once the toolbox is installed, type

on the Matlab command prompt to open the list of demos, or access the page from the Matlab Help/TOAST Toolbox/TOAST Demos link.

More info about the demos is available here.

Matlab online tutorials

Below is a list of online tutorials shows typical use examples for the Matlab-Toast toolbox. Each tutorial contains a link to the Matlab script to recreate the example.

The tutorials introduce the concept of the forward and inverse problems in optical tomography step by step. It is recommended to work through them in sequence, since later tutorials build upon the previous ones.

Mesh generation for Toast problems with Gmsh

Mesh generation - Tutorial 1: Build a spherical mesh

Create a spherical mesh with the Gmsh user interface, and import it into Toast.

Mesh generation - Tutorial 2: Adding internal structure to the sphere

Create a sphere with multiple regions by adding internal surfaces.

Mesh generation - Tutorial 3: Creating an adaptive mesh

Create an adaptive mesh based on a nodal density function

Solving DOT forward problems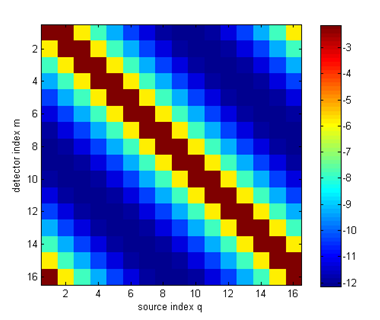

Tutorial 1: Building a DOT forward solver

This example shows a basic forward solver for a simple 2-D homogeneous problem, generating steady-state boundary data. It explains how to create a mesh, set up homogeneous parameter vectors, define the source and detector profiles, and solve the linear FEM problem.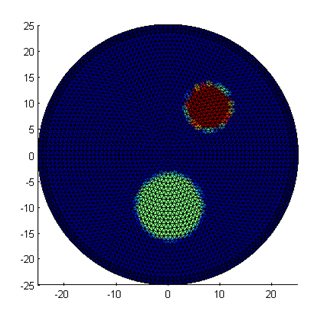

Tutorial 2: Extending to inhomogeneous parameters

This example shows how to define inhomogeneous parameter distributions by mapping bitmap images into the mesh basis, and evaluates the data differences to the homogeneous solution.

Tutorial 3: Generating frequency-domain data

This example applies modifications to the script to allow for the calculation of complex-valued measurement data from modulated light sources.

Tutorial 4: Generating time-domain data

This example shows how to solve the time-dependent diffusion equation by applying a finite-difference scheme to represent the time derivative. It shows the setup of the system matrices and the solver loop for the time steps.

Tutorial 5: Non-uniqueness

Simultaneous reconstruction of the absorption and scattering parameters requires sufficient information in the measurement data to distinguish between the effects of the parameters. This example shows that steady-state intensity data do not allow to reconstruct for both parameter distributions.

Tutorial 6: Constructing the Jacobian matrix

The Jacobian defines the derivative of the forward operator with respect to given parameter distributions. It is an important element of many reconstruction algorithms. This example shows how to calculate the Jacobian, and the interpretation of individual rows as photon measurement density functions.