 balls of the first colour,
balls of the first colour, 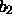 of the second colour and so on to
of the second colour and so on to  balls of the last colour,
is given by a multinomial distribution
balls of the last colour,
is given by a multinomial distribution
If a program's length does not obey l=2n+4i-1 then it cannot be a solution to the order n parity problem and will score exactly half marks on the parity problems. If l=2n+4i-1 is true there is a chance that a randomly generated program will contain an odd number of each input and so be a solution.
When calculating the fraction of programs of a given length that are solutions we can ignore the number of different tree shapes because whether a tree is a solution or not is determined only by how we label its leafs and not by its shape.
The proportion of trees of length l which are parity solutions is
the same as the chance of choosing at random t coloured balls, with
reselection, from a bag containing equal numbers of each n-coloured
balls, in such away that we have an odd number of all n-colours.
(The proportion which are solutions to the always-on or always-off problems are the
chance that we have an even number of all n-colours).
The probability of drawing  balls of the first colour,
balls of the first colour, 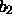 of the second colour and so on to
of the second colour and so on to  balls of the last colour,
is given by a multinomial distribution
balls of the last colour,
is given by a multinomial distribution

While drawing each ball is an independent event, the chance of having an odd number of one colour is not independent of the chance that we have an odd number of a different colour. This is because we are drawing exactly t balls and so the sum of each colour must come to t. Calculating these probabilities and summing them is tedious but we can derived a limit for behaviour as the number of balls becomes large.
Consider first one colour (one terminal, e.g. D0).
The chance of drawing an odd number of them from the bag in t trials
is
 (where
(where 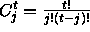 ).
I.e. the sum of all the odd terms in a binomial distribution.
As the number of trials in a binomial distribution is increased it
becomes increasingly smooth.
(In the limit it approaches the Gaussian distribution, with a central
peak at
).
I.e. the sum of all the odd terms in a binomial distribution.
As the number of trials in a binomial distribution is increased it
becomes increasingly smooth.
(In the limit it approaches the Gaussian distribution, with a central
peak at 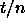 and a standard deviation of
and a standard deviation of  ).
If
).
If 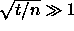 then each term in the binomial expansion is close
to its neighbour, i.e. each odd term is close to an even term so
then each term in the binomial expansion is close
to its neighbour, i.e. each odd term is close to an even term so
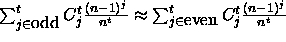 and since
and since
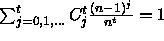 so
so
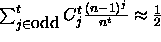 and
and
 .
.
The total number of each of the colours must sum to t.
This reduces the number of degrees of freedom by one,
i.e. given the oddness of the number of balls of n-1
colours the oddness of the number of the remaining colour is fixed.
Thus
the total probability that there will be an odd number of each colour
is the product of  rather than n independent events,
i.e.
rather than n independent events,
i.e. 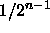 .
Likewise the probability of an even number of every colour will
also tend to
.
Likewise the probability of an even number of every colour will
also tend to 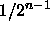 as t increases.
([Fenner1998]
has a formal proof of this result using a Markov chain analysis).
as t increases.
([Fenner1998]
has a formal proof of this result using a Markov chain analysis).
Figure 1 shows the fraction of 100,000 random programs
which are solutions to the Even-6 parity or always-on-6 problems, for
a variety of lengths.
Figure 1 shows measurement approaches the theoretical large
program limit closely for 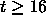 , i.e.
, i.e. 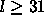 .
.
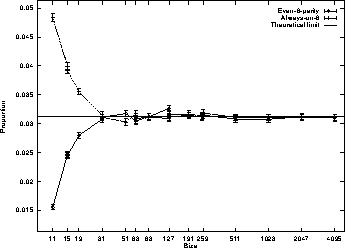
Figure 1:
Fraction of programs that solve Even-6 parity or Always-on-6 problems,
using EQ
(note log scale).
Error bars show standard error.
Figure 2 shows the fraction of random programs
which are solutions to the Even or Odd parity problems
(100,000 or a million random trials).
The lengths of the programs were chosen so that
l=2n+4i-1 is true and the number of leafs exceeds
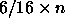 .
Figure 2 again shows agreement between measurement
and the theoretical large program limit.
.
Figure 2 again shows agreement between measurement
and the theoretical large program limit.
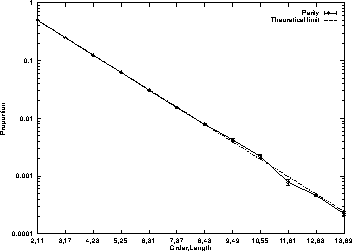
Figure 2:
Fraction of programs that solve parity problems given appropriate
building block.
Length of programs increases with problem order so
 .
.