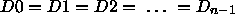 . However given the symmetry of the
EQ building block the inputs to the program can occur in any order.
Further
. However given the symmetry of the
EQ building block the inputs to the program can occur in any order.
Further 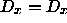 is true so
is true so 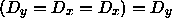 therefore any pair of repeated inputs can be removed from the program
without changing its output.
therefore any pair of repeated inputs can be removed from the program
without changing its output.
Even parity solutions, where n is even, are of the form
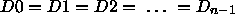 . However given the symmetry of the
EQ building block the inputs to the program can occur in any order.
Further
. However given the symmetry of the
EQ building block the inputs to the program can occur in any order.
Further 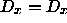 is true so
is true so 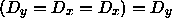 therefore any pair of repeated inputs can be removed from the program
without changing its output.
therefore any pair of repeated inputs can be removed from the program
without changing its output.
Odd parity solutions, where n is odd, are of the form
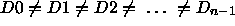 .
Again given the symmetry of the
XOR building block the inputs to the program can occur in any order.
Further
.
Again given the symmetry of the
XOR building block the inputs to the program can occur in any order.
Further 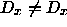 is false but
is false but  so
so 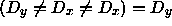 therefore again any pair of repeated inputs can be removed from the program
without changing its output.
therefore again any pair of repeated inputs can be removed from the program
without changing its output.
Therefore any program will be a solution to the parity problem
provided it contains an odd number of all n terminals.
Thus all solutions contain t=n+2i, where 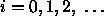 ,
terminals.
Both EQ and XOR are binary functions, so programs
are of odd length l = 2t-1 and
solutions
are of length l=2t-1=2n+4i-1.
,
terminals.
Both EQ and XOR are binary functions, so programs
are of odd length l = 2t-1 and
solutions
are of length l=2t-1=2n+4i-1.
Any program with an even number of one or more inputs effectively ignores those inputs. Given the nature of the parity function, such a program will pass exactly half the fitness cases.
The always-on function effectively ignores all its inputs.
When n is even this can only be implemented by having an even number
of all inputs. If there are an odd number of any input,
then the function will return true in exactly half the fitness cases.
If n is odd, always-on cannot be implemented using the available
primitives (XOR and 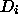 ) however the analogous
function always-off can and like always-on (for the n even case)
requires there to be an even number of each input. Otherwise it
returns false in exactly half the fitness cases.
) however the analogous
function always-off can and like always-on (for the n even case)
requires there to be an even number of each input. Otherwise it
returns false in exactly half the fitness cases.