


Next: Parity and Always-on/off
Up: Why ``Building Blocks'' Don't
Previous: Introduction
The program trees we will consider are composed of n terminals
(D0, D1, ... D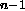 ) which are the Boolean inputs to the program
and the Boolean logic functions EQ or XOR
[Koza1992].
(D0, D1, ... D
) which are the Boolean inputs to the program
and the Boolean logic functions EQ or XOR
[Koza1992].
(D0, D1, ... D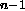 ) and EQ
are sufficient to create an even-n parity function, when n is even and
likewise (D0, D1, ... D
) and EQ
are sufficient to create an even-n parity function, when n is even and
likewise (D0, D1, ... D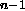 ) and XOR are sufficient
to create an odd-n parity function
if n is odd.
(Odd parity solutions can be readily converted to even parity by
inverting the final output of the program.
For simplicity we don't require the final negation
and instead consider programs with only one type of function).
The fitness of each tree is given by evaluating it as a logical
expression for each of the
) and XOR are sufficient
to create an odd-n parity function
if n is odd.
(Odd parity solutions can be readily converted to even parity by
inverting the final output of the program.
For simplicity we don't require the final negation
and instead consider programs with only one type of function).
The fitness of each tree is given by evaluating it as a logical
expression for each of the 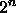 possible combinations of D
possible combinations of D inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
There are
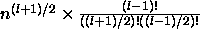 different trees of length l
[Koza1992, page 213,] [Alonso and Schott1995].
The number of programs rises rapidly (approximately
exponentially) with increasing program length l.
Of course if no bounds are placed on the size or depth of programs
then the number of them is unbounded,
i.e. the search space is infinite.
different trees of length l
[Koza1992, page 213,] [Alonso and Schott1995].
The number of programs rises rapidly (approximately
exponentially) with increasing program length l.
Of course if no bounds are placed on the size or depth of programs
then the number of them is unbounded,
i.e. the search space is infinite.
William B Langdon
Mon Jul 13 15:53:27 BST 1998
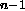 ) which are the Boolean inputs to the program
and the Boolean logic functions EQ or XOR
[Koza1992].
(D0, D1, ... D
) which are the Boolean inputs to the program
and the Boolean logic functions EQ or XOR
[Koza1992].
(D0, D1, ... D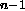 ) and EQ
are sufficient to create an even-n parity function, when n is even and
likewise (D0, D1, ... D
) and EQ
are sufficient to create an even-n parity function, when n is even and
likewise (D0, D1, ... D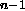 ) and XOR are sufficient
to create an odd-n parity function
if n is odd.
(Odd parity solutions can be readily converted to even parity by
inverting the final output of the program.
For simplicity we don't require the final negation
and instead consider programs with only one type of function).
The fitness of each tree is given by evaluating it as a logical
expression for each of the
) and XOR are sufficient
to create an odd-n parity function
if n is odd.
(Odd parity solutions can be readily converted to even parity by
inverting the final output of the program.
For simplicity we don't require the final negation
and instead consider programs with only one type of function).
The fitness of each tree is given by evaluating it as a logical
expression for each of the 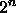 possible combinations of D
possible combinations of D inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
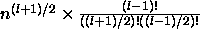 different trees of length l
[
different trees of length l
[