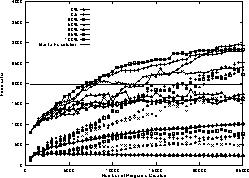
Figure 16: Evolution of maximum, population mean and standard deviation of food eaten on all 50 trails as plagiarism penalty is increased. Means of 10 runs.
This section reports results from 50 independent runs with each plagiarism penalty setting. As in Sect. 4 the same initial populations are used with each plagiarism value. Some of the differences between this section and Sect. 4 are due to the larger number or runs made, which reduces the influence of stochastic effects.
To gain a measure of the ability of GP to generalise from the example trials, the populations where also tested on the complete set of 50 trails and statistics for the complete set were gathered. This information is used only for reporting purposes and only the current (and previous) trails influence the course of evolution. (As running all programs on all 50 trails is CPU expensive, this data was only collected for the first ten of the 50 runs in each experiment).
Figure 3 shows the evolution of scores using the new dynamic fitness function. Much of the variation between one generation and the next can be ascribed to the different difficulty of the trials. If we consider Fig. 16 we see rather more monotonic rises in program score. Referring to Fig. 3 again, with 50 program runs, we can see a clear separation into runs with low penalty performing approximately 6--9 food pellets better than those with high penalties. This difference is amplified if instead of looking at average performance, we look at the number of runs where at least one solution to the current trail was found, cf. Fig. 17.

Figure 16:
Evolution of maximum, population mean and standard deviation of food eaten
on all 50 trails
as plagiarism penalty is increased.
Means of 10 runs.
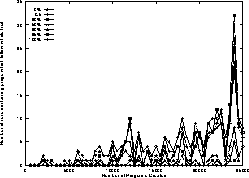
Figure 17:
Number of populations containing a solution to current trail
on random trails
as plagiarism penalty is increased.
50 runs.
The random trails seem to be a harder problem than the Santa Fe trail, only three runs
evolved programs which could follow all 50 trails. Another aspect of this increased difficulty is the evolved solution given in [Koz92, page 154,] to the Santa Fe trail scores less than half marks on the random trails. In contrast each of the first programs found which could pass all 50 random trails can also follow the Santa Fe trail.
There is some evidence that the random trails are themselves enough to
avoid convergence of the GP population.
If we look at the fraction of the population created before the first
best of generation program is found,
cf. Fig. 7,
even without a penalty it remains near 100 (i.e. 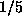 ) rather than
falling to near one.
With a penalty then it remains near to 200 (like the runs with large
or modest penalties on the Santa Fe trail).
However lack of convergence would suggest that the fraction of
children behaving as their parents would be small,
whereas it behaves similarly to the Santa Fe runs
and with low penalties (20% or less) the fraction rises to about 80%
by the end of the run
(cf. Fig. 9).
With higher penalties the fraction also behaves like the Santa Fe runs
and remains near its initial value until the end of the runs.
Again variety is near unity and does not show this convergence at all.
(With no penalty then variety reaches 97% on
average at generation 50
and with a penalty it is about 95% on average again).
) rather than
falling to near one.
With a penalty then it remains near to 200 (like the runs with large
or modest penalties on the Santa Fe trail).
However lack of convergence would suggest that the fraction of
children behaving as their parents would be small,
whereas it behaves similarly to the Santa Fe runs
and with low penalties (20% or less) the fraction rises to about 80%
by the end of the run
(cf. Fig. 9).
With higher penalties the fraction also behaves like the Santa Fe runs
and remains near its initial value until the end of the runs.
Again variety is near unity and does not show this convergence at all.
(With no penalty then variety reaches 97% on
average at generation 50
and with a penalty it is about 95% on average again).
The lower covariance of length and fitness in the initial populations compared to the Santa Fe trail is surprising (comparing Fig. 10 and Fig. 11). Possibly it is simply due to some difference between the first random trail and the Santa Fe trail. Comparing Fig. 11 with Fig. 10 we see there is no longer a clear separation between runs based upon strength of plagiarism penalty. After generation 15 low penalty runs tend to have smaller covariances than with the Santa Fe trail. This is reflected in the generally lower increase in program size. The lower covariance may be simply due to increased randomness in the fitness function. In contrast when we look at the correlation between score and size (i.e. excluding penalty, cf. Fig. 13) the high penalty runs have an obviously lower correlation. This shows that the penalty has changed the nature of the evolved programs. Striking confirmation for this is given in Fig. 15, which shows with the dynamic fitness function and a high plagiarism penalty, programs with very different behaviour evolve than is the case with the Santa Fe trail or with low penalty.
The large number of ant operations per program execution (cf. Fig. 15) might indicate that non-general, or trail specific, programs have been evolved. This is confirmed in that the best scores (averaged over 50 runs) in the last generation are between 66% (100% penalty) and and 81% (20% penalty) for the last trail (cf. Fig. 3) but the best programs in the same populations (averaged over 10 runs) only score 40% (100% penalty) to 73% (0% penalty) when tested on all 50 trails (cf. Fig. 16). That is populations evolved with high plagiarism penalties do considerably better on the immediate training case than they do on the more general one. The difference is not so marked in runs with low penalties.
Considering successful crossovers is more difficult when the fitness function changes as most improvements in performance stem from decreases in the difficulty of the training case from one generation to the next. However in the first ten runs with no penalty there were on average 5,825.5 successful crossovers
and 4,933.2 with 100% penalty. In low penalty runs improvements are found mainly in generations with easier tests but they are spread more widely in high penalty runs.
The scores of parents with dynamic test cases behaves like those with the Santa Fe trail. I.e. runs with low penalties show convergence in that (in all but one of the first ten runs) the scores of the parents of all (or the vast majority) of the children in the last generation are identical (or have one of two values). With runs with high penalty there is more variation (with on average 29.1 different scores acting as first parents to children in the final population).