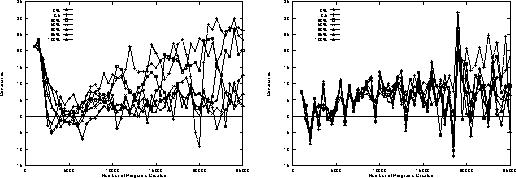
Figure 11: Evolution of covariance of program length and normalised rank based fitness on random trails as plagiarism penalty is increased. Means of 50 runs.
In GP program size is inherited and so we can apply Price's Covariance and Selection Theorem [Pri70] to it. Provided our genetic operators are unbiased with respect to length, the expected change in mean program length from one generation to the next is given by the covariance between program length and normalised fitness in the previous generation. (Normal GP crossover is unbiased provided size or depth restrictions don't effect the population [LP97]). Figure 10 shows in the first few generations there is a strong covariance between length and fitness. We suggest this is because in the initial random populations long programs tend to do better simply because they are more likely to contain useful primitives such as Move. In the next few generations strong selection acts to remove useless programs and consequently the covariance falls. The plagiarism penalty appears to dilute this effect of selection so the covariance in high penalty runs takes more generations to fall. There is then a period of about eight generations during which crossover finds many improved solutions and covariance remains small after which the normal increase is seen in low penalty runs and the populations bloat. However Fig. 10 shows strong plagiarism penalties appear to prevent the covariance increasing towards the end of the runs so reducing the bloat seen with low penalties (cf. Fig. 4). However the covariance remains positive and some increase in programs size is seen even with the highest penalty.

Figure 11:
Evolution of covariance of program length and normalised rank based fitness
on random trails
as plagiarism penalty is increased.
Means of 50 runs.
Figure 10:
Evolution of covariance of program length and normalised rank based fitness
on Santa Fe trail
as plagiarism penalty is increased.
Means of 10 runs.
Figure 12 plots the correlation coefficient of program size
and amount of food eaten.
(Correlation coefficients are equal to the covariance after it has
been normalised to lie in the range 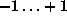 .
By considering food eaten we avoid the intermediate stage of
converting program score to expected number of children
required when applying Price's Theorem
and exclude the plagiarism penalty).
Figure 12 shows in all cases
there is a positive correlation between
program score (rather than fitness)
and length of programs.
This correlation does not vary strongly with the plagiarism penalty.
.
By considering food eaten we avoid the intermediate stage of
converting program score to expected number of children
required when applying Price's Theorem
and exclude the plagiarism penalty).
Figure 12 shows in all cases
there is a positive correlation between
program score (rather than fitness)
and length of programs.
This correlation does not vary strongly with the plagiarism penalty.
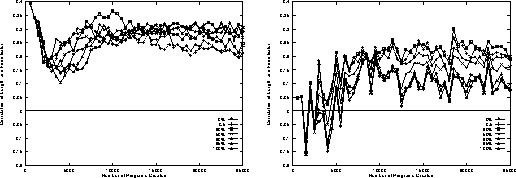
Figure 13:
Correlation of program length and food eaten
on random trails
as plagiarism penalty is increased.
Means of 50 runs.
Figure 12:
Correlation of program length and food eaten
on Santa Fe trail
as plagiarism penalty is increased.
Means of 10 runs.