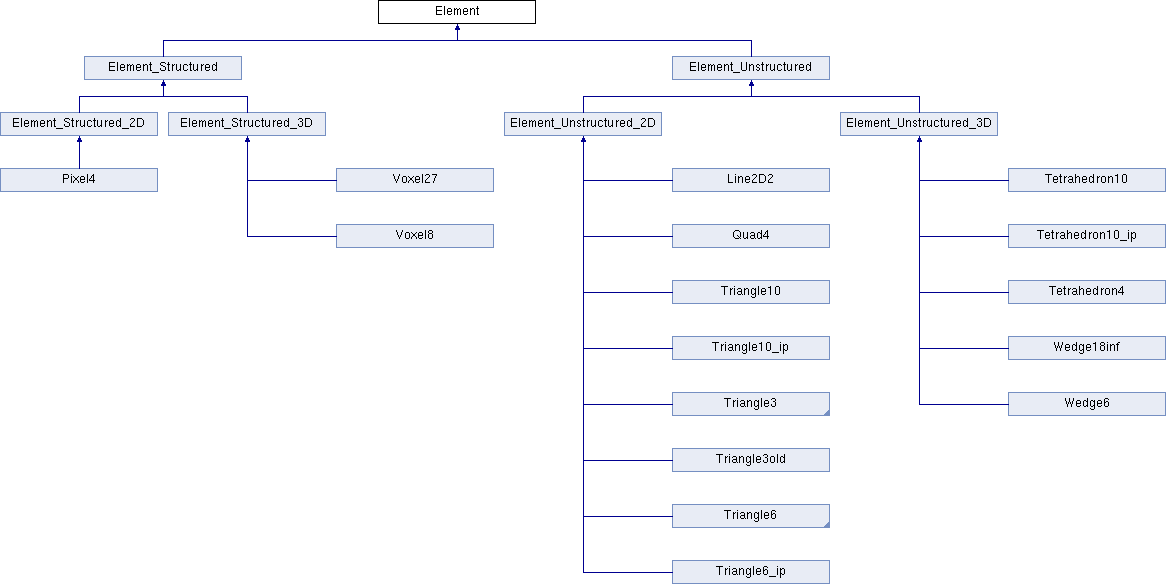
Base class for finite element types. More...

#include <element.h>

Inheritance diagram for Element:

Public Member Functions
	Element ()
	Creates a new element with no nodes.

	Element (const Element &el)
	Creates a new element as a copy of 'el'.

virtual	~Element ()
	Destroys the element.

virtual Element *	Copy ()=0
	Create a copy of the element and return a pointer to it.

virtual void	Initialise (const NodeList &nlist)
	Element initialisation. More...

virtual void	PostInitialisation (const NodeList &nlist)
	Element setup after mesh initialisation. More...

void	operator= (const Element &el)
	Element assignment. More...

virtual BYTE	Type () const =0
	Returns an element type identifier. More...

virtual BYTE	VtkType () const
	Returns the VTK element type identifier, or 0 if the element doesn't have a VTK representation.

virtual unsigned long	GetCaps () const =0
	Returns element capability flags. More...

virtual int	Dimension () const =0
	Returns the spatial dimension of the element. More...

virtual int	nNode () const =0
	Returns the number of nodes associated with the element. More...

virtual int	nSide () const =0
	Returns the number of element sides. More...

virtual int	nSideNode (int side) const =0
	Returns the number of vertices associated with a side. More...

virtual int	SideNode (int side, int node) const =0
	Returns relative node index for a side vertex. More...

virtual bool	IsNode (int node)
	Checks if a node is part of the element. More...

int	IsSide (int nn, int *nd)
	Checks if a face defined by vertex nodes is part of the element. More...

virtual bool	IsSideNode (int side, int node)
	Checks if a node is associated with a specific side. More...

bool	IsBoundarySide (int side)
	Checks if a side is on the mesh surface. More...

bool	HasBoundarySide ()
	Checks if the element contains any surface sides. More...

bool	HasInterfaceSide ()
	Checks if the element contains any internal interface sides. More...

virtual Point	Local (const NodeList &nlist, const Point &glob) const =0
	Maps a point from global to local element coordinates. More...

virtual Point	NodeLocal (int node) const =0
	Returns the local coordinates of an element node. More...

virtual Point	SurfToLocal (int side, const Point &p) const
	Maps a point from surface coordinates to local element coordinates. More...

virtual void	MapToSide (int side, Point &loc) const
	Translates a point to an element surface. More...

virtual Point	SideCentre (int side) const
	Returns the centre point of a side. More...

Element *	SideNeighbour (int side) const
	returns a pointer to the element connected at 'side', or NULL if this is a boundary side. More...

int	SideNeighbourIndex (int side) const
	Returns the list index of the element connected at 'side', or -1 if this is a boundary side. More...

Point	Global (const NodeList &nlist, const Point &loc) const
	Maps a point from local element coordinates to global coordinates. More...

virtual RDenseMatrix	Elgeom (const NodeList &nlist) const
	Returns the element's global node coordinates. More...

virtual RVector	DirectionCosine (int side, RDenseMatrix &jacin)=0
	Returns the direction cosines of a side normal. More...

virtual const RVector &	LNormal (int side) const =0
	Returns a side normal in local coordinates. More...

virtual double	Size () const =0
	Returns the element size. More...

virtual double	SideSize (int side, const NodeList &nlist) const
	Returns the size of an element side. More...

virtual double	DetJ (const Point &loc, const NodeList *nlist=0) const
	Returns determinant of Jacobian at a given point inside the element in the local frame. More...

virtual bool	LContains (const Point &loc, bool pad=true) const =0
	Checks if a local point coordinate is inside the element. More...

virtual bool	GContains (const Point &glob, const NodeList &nlist) const
	Checks if a global point coordinate is inside the element. More...

virtual int	BndSideList (const NodeList &nlist, int *list)
	Returns a list of boundary sides. More...

void	InitNeighbourSupport ()

void	InitSubdivisionSupport ()

int	SubdivisionLevel () const
	Returns the element's subdivison level. More...

virtual void	Subdivide (Mesh *mesh)

virtual RVector	LocalShapeF (const Point &loc) const =0
	Returns the values of the shape functions at a local point. More...

virtual RDenseMatrix	LocalShapeD (const Point &loc) const =0
	Returns the values of the shape function derivatives at a local point. More...

virtual RVector	GlobalShapeF (const NodeList &nlist, const Point &glob) const
	Returns the values of the shape functions at a global point. More...

virtual RDenseMatrix	GlobalShapeD (const NodeList &nlist, const Point &glob) const
	Returns the values of the shape function derivatives at a global point. More...

virtual int	QuadRule (int order, const double wght, const Point absc) const
	Returns the weights and abscissae of quadrature rules over the element. More...

virtual double	IntF (int i) const =0
	Integral of a shape function over the element. More...

virtual RSymMatrix	IntFF () const =0
	Integrals of all products of two shape functions over the element. More...

virtual double	IntFF (int i, int j) const =0
	Integral of a product of two shape functions over the element. More...

virtual double	IntFFF (int i, int j, int k) const =0
	Integral of a product of three shape functions over the element. More...

virtual RSymMatrix	IntPFF (const RVector &P) const =0
	Integrals of all products of two shape functions and a nodal function over the element. More...

virtual double	IntPFF (int i, int j, const RVector &P) const =0
	Integral of a product of two shape functions and a nodal function over the element. More...

virtual RSymMatrix	IntDD () const =0
	Integrals of all products of two shape function derivatives over the element. More...

virtual double	IntDD (int i, int j) const =0
	Integral of a product of two shape function derivatives over the element. More...

virtual RVector	IntFD (int i, int j) const
	Integral of a product of a shape function and a shape function derivative over the element. More...

virtual double	IntFDD (int i, int j, int k) const =0
	Integral of a product of a shape function and two shape function derivatives over the element. More...

virtual RSymMatrix	IntPDD (const RVector &P) const =0
	All integrals of products of a nodal function and two shape function derivatives over the element. More...

virtual double	IntPDD (int i, int j, const RVector &P) const =0
	Integrals of a product of a nodal function and two shape function derivatives over the element. More...

virtual RVector	BndIntF () const
	Boundary integral of all shape functions over all boundary sides of the element. More...

virtual double	BndIntFSide (int i, int sd)
	Surface integral of a shape function over one of the sides of the element. More...

virtual RSymMatrix	BndIntFF () const =0
	Boundary integral of all products of two shape functions over all boundary sides of the element. More...

virtual double	BndIntFF (int i, int j)=0
	Boundary integral of a product of two shape functions over all boundary sides of the element. More...

virtual double	BndIntFFSide (int i, int j, int sd)=0
	Surface integral of a product of two shape functions over one of the sides of the element. More...

virtual RSymMatrix	BndIntPFF (const RVector &P) const =0
	Surface integrals of all products of a nodal function and two shape functions over all boundary sides of the element. More...

virtual double	BndIntPFF (int i, int j, const RVector &P) const =0
	Surface integrals of a product of a nodal function and two shape functions over all boundary sides of the element. More...

virtual double	Intd (int i, int k) const
	Integral of partial shape function derivative over the element. More...

virtual double	IntFd (int i, int j, int k) const
	Integral of the product of a shape function and a partial shape function derivative over the element. More...

virtual double	IntPd (const RVector &P, int j, int k) const
	Integral of the product of a nodal function and a partial shape function derivative over the element. More...

virtual RSymMatrix	Intdd () const
	Integral of the product of two partial shape function derivatives over the element. More...

virtual double	IntFdd (int i, int j, int k, int l, int m) const
	Integral of the product of a shape function and two partial shape function derivatives over the element. More...

virtual double	IntPdd (const RVector &p, int j, int k, int l, int m) const

virtual double	IntFfd (int i, int j, int k, int l) const

virtual double	IntPfd (const RVector &p, int j, int k, int l) const

virtual double	IntUnitSphereP (const NodeList &nlist, const RVector &P) const

virtual double	IntUnitSphereFF (const NodeList &nlist, const int i, const int j) const

virtual double	IntUnitSpherePFF (const NodeList &nlist, const int i, const int j, const RVector &P) const

virtual RVector	BndIntFX (int side, double(*func)(const Point &), const NodeList &nlist) const

virtual RVector	BndIntFCos (int side, const Surface *surf, const RVector &cntcos, double sigma, double sup, const NodeList &nlist) const

virtual RVector	BndIntFCos (int side, const RVector &cntcos, double a, const NodeList &nlist) const

virtual RVector	BndIntFDelta (int side, const Surface *surf, const RVector &pos, const NodeList &nlist) const

int	GetSubsampleFD (int &n, double &wght, Point &absc, RVector &F, RDenseMatrix &D, const NodeList &nlist) const

int	GetBndSubsampleFD (int side, int &n, double &wght, Point &absc, RVector &F, RDenseMatrix &D, const NodeList &nlist) const

virtual int	GetLocalSubsampleAbsc (const Point *&absc) const

virtual int	GetBndSubsampleAbsc (int side, const Point *&absc) const

virtual RDenseMatrix	StrainDisplacementMatrix (const Point &glob) const

virtual RDenseMatrix	ElasticityStiffnessMatrix (const RDenseMatrix &D) const

virtual RDenseMatrix	ElasticityStiffnessMatrix (double E, double nu) const

RDenseMatrix	ElasticStrainDisplacement (const RVector &loc, const RDenseMatrix &gder) const

virtual RDenseMatrix	IsotropicElasticityMatrix (double E, double nu) const

virtual RVector	InitialStrainVector (double E, double nu, const RVector &e0)

virtual RVector	ThermalExpansionVector (double E, double nu, double alpha, double dT)

virtual RVector	DThermalExpansionVector (double E, double nu)

virtual int	GlobalIntersection (const NodeList &nlist, const Point &p1, const Point &p2, Point **list)=0

virtual int	Intersection (const Point &, const Point &, Point **)=0

virtual RDenseMatrix	LocaltoGlobalMat () const

virtual RDenseMatrix	GlobaltoLocalMat () const

virtual RDenseMatrix	FTAMat () const

int	Region () const

void	SetRegion (int nr)

virtual void	SplitSide (Mesh mesh, int side, int newnode, Element nbr1, Element nbr2, Element el1, Element *el2)

virtual void	Bisect (Mesh mesh, int side, int newnode, Element nbr1, Element nbr2, Element el1, Element *el2)

virtual void	MergeAndResplit (Mesh mesh, int side, int newnode, Element nbr1, Element nbr2, Element el1, Element *el2)

Public Attributes
int *	Node

ElementSubdivisionData *	subdivdata

Element **	sdnbhr

int *	sdnbhridx

Protected Attributes
bool *	bndside

bool	bndel

bool	interfaceel

int	region

Friends
class	ElementList

class	Mesh

std::istream &	operator>> (std::istream &i, Element &el)

std::ostream &	operator<< (std::ostream &o, const Element &el)

Detailed Description

Base class for finite element types.

This class defines the common interface for all Toast FEM elements, in particular a set of integrals of combinations of shape function, shape function derivatives and nodal functions over the element (Int*).

Member Function Documentation

virtual RVector Element::BndIntF ( ) const

inlinevirtual

Boundary integral of all shape functions over all boundary sides of the element.

Returns: Vector of size nNode, containing the integrals
$\int_{\partial\Omega} u_i(\vec{r}) d\vec{r}$
where the integration is performed over all sides of teh element that are part of the mesh surface.

Note: The returned matrix contains nonzero entries at index i only if node i is a boundary node.; If the element does not contain boundary sides, the returned vector is zero.

See Also: BndIntFSide, BndIntFF, BndIntFFSide

Reimplemented in Tetrahedron4.

virtual RSymMatrix Element::BndIntFF ( ) const

pure virtual

Boundary integral of all products of two shape functions over all boundary sides of the element.

Returns: Matrix of size nNode x nNode, containing the integrals
$\int_{\partial\Omega} u_i(\vec{r}) u_j(\vec{r}) d\vec{r}$
where the integration is performed over all sides of the element that are part of the mesh surface.

Note: The returned matrix contains nonzero entries at (i,j) only if nodes i and j are both boundary nodes.; If the element does not contain boundary sides, the returned matrix is zero.

See Also: BndIntFF(int,int), BndIntFFSide

Implemented in Element_Unstructured, Pixel4, Voxel8, and Voxel27.

virtual double Element::BndIntFF	(	int	i,
		int	j
	)

pure virtual

Boundary integral of a product of two shape functions over all boundary sides of the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)

Returns: Value of the integral
$\int_{\partial\Omega} u_i(\vec{r}) u_j(\vec{r}) d\vec{r}$
where the integration is performed over all sides of the element that are part of the mesh surface.

Note: The return value is nonzero only if both nodes i and j are boundary nodes.

See Also: BndIntFF()const, BndIntFFSide

Implemented in Element_Unstructured, Pixel4, Voxel8, and Voxel27.

virtual double Element::BndIntFFSide	(	int	i,
		int	j,
		int	sd
	)

pure virtual

Surface integral of a product of two shape functions over one of the sides of the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)
sd	side index (range 0 .. nSide-1)

Returns: Value of the integral
$\int_{\partial\Omega} u_i(\vec{r}) u_j(\vec{r}) d\vec{r}$
where the integration is performed over side sd.

Note: Nodes i and j must both belong to side sd.

See Also: BndIntFF()const, BndIntFF(int,int)

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Pixel4, Wedge6, Triangle6, Voxel8, Triangle10, Voxel27, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

virtual double Element::BndIntFSide	(	int	i,
		int	sd
	)

inlinevirtual

Surface integral of a shape function over one of the sides of the element.

Parameters

i	node index (range 0 .. nNode-1)
sd	side index (range 0 .. nSide-1)

Returns: Value of the integral
$\int_{\partial\Omega} u_i(\vec{r}) d\vec{r}$
where the integration is performed over side sd.

See Also: BndIntF, BndIntFF, BndIntFFSide

Reimplemented in Triangle3, Tetrahedron4, Triangle6, and Triangle10.

virtual RSymMatrix Element::BndIntPFF ( const RVector & P ) const

pure virtual

Surface integrals of all products of a nodal function and two shape functions over all boundary sides of the element.

Parameters

P	nodal function coefficients over the mesh

Returns: Matrix of size nNode x nNode, containing the integrals
$\int_{\partial\Omega} p(\vec{r}) u_i(\vec{r}) u_j(\vec{r}) d\vec{r} = \sum_k p_k \int_{\partial\Omega} u_i(\vec{r}) u_j(\vec{r}) u_k(\vec{r}) d\vec{r}$

Note: If the element does not contain boundary sides, the returned matrix is zero.

See Also: BndIntPFF(int,int,const RVector&)const, BndIntFF

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Pixel4, Wedge6, Voxel8, Triangle6, Triangle10, Voxel27, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

virtual double Element::BndIntPFF	(	int	i,
		int	j,
		const RVector &	P
	)		const

pure virtual

Surface integrals of a product of a nodal function and two shape functions over all boundary sides of the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)
P	nodal function coefficients over the mesh

Returns: Value of the integral
$\int_{\partial\Omega} p(\vec{r}) u_i(\vec{r}) u_j(\vec{r}) d\vec{r} = \sum_k p_k \int_{\partial\Omega} u_i(\vec{r}) u_j(\vec{r}) u_k(\vec{r}) d\vec{r}$

Note: If the element does not contain boundary sides, the returned matrix is zero.

See Also: BndIntPFF(const RVector&)const, BndIntFF

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Pixel4, Wedge6, Triangle6, Voxel8, Triangle10, Voxel27, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

virtual int Element::BndSideList	(	const NodeList &	nlist,
		int *	list
	)

virtual

Returns a list of boundary sides.

Parameters

nlist	mesh node list
address	of list to be filled with boundary side indices

Returns: Number of boundary sides in the element.

Note: This method fills array list with side indices (>= 0) of all boundary sides associated with the element.; list must have been allocated by the caller with sufficient length to receive all boundary side indices.

Bug:

This method assumes that a side is a boundary side if all its associated nodes are boundary nodes. This is not always correct, in particular at corners.

See Also: IsBoundarySide, HasBoundarySide, IsSideNode

virtual double Element::DetJ	(	const Point &	loc,
		const NodeList *	nlist = `0`
	)		const

inlinevirtual

Returns determinant of Jacobian at a given point inside the element in the local frame.

Parameters

loc	evaluation point in local coordinates
nlist	node list of the associated mesh

Returns: det(J)

Reimplemented in Triangle3, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, and Tetrahedron4.

virtual int Element::Dimension ( ) const

pure virtual

Returns the spatial dimension of the element.

Returns: 2 for 2-D elements (triangles, pixels etc.), 3 for 3-D elements (tetrahedra, voxels, etc.)

Implemented in Element_Unstructured_3D, Element_Unstructured_2D, Element_Structured_3D, Element_Structured_2D, Triangle3D6, and Triangle3D3.

virtual RVector Element::DirectionCosine	(	int	side,
		RDenseMatrix &	jacin
	)

pure virtual

Returns the direction cosines of a side normal.

Parameters

side	side index (>= 0)
jacin	inverse of Jacobian

Returns: direction cosines of the normal to side in global coordinates.

See Also: LNormal

Implemented in Triangle3, Line2D2, Triangle3D6, Tetrahedron4, Triangle10, Triangle3D3, Triangle6, Voxel8, Triangle3old, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, and Wedge6.

virtual RDenseMatrix Element::Elgeom ( const NodeList & nlist ) const

virtual

Returns the element's global node coordinates.

Parameters

nlist mesh node list

Returns: Global node coordinates in an nNode x Dimension matrix.

Note: This method extracts the coordinates of the nodes associated with the element from nlist and returns them as a dense matrix.

virtual bool Element::GContains	(	const Point &	glob,
		const NodeList &	nlist
	)		const

virtual

Checks if a global point coordinate is inside the element.

Parameters

glob	point in global coordinates
nlist	mesh node list

Returns: true if the point is inside the element, false otherwise.

See Also: LContains

Reimplemented in Element_Unstructured, Triangle3, Triangle3D6, Line2D2, Triangle3D3, Triangle10, Triangle3old, Triangle6, Voxel8, Voxel27, Pixel4, Triangle10_ip, Triangle6_ip, and Quad4.

virtual unsigned long Element::GetCaps ( ) const

pure virtual

Returns element capability flags.

Returns: Bitflags for element caps. (see Element capability flags)

Implemented in Triangle3, Tetrahedron4, Triangle10, Triangle6, Voxel8, Tetrahedron10_ip, Tetrahedron10, Voxel27, Line2D2, Pixel4, Triangle10_ip, Triangle6_ip, Quad4, Triangle3old, and Wedge6.

Point Element::Global	(	const NodeList &	nlist,
		const Point &	loc
	)		const

Maps a point from local element coordinates to global coordinates.

Parameters

nlist	mesh node list
loc	point in local element coordinates

Note: Point loc should have dimension Dimension(); loc does not have to be located inside the element.

See Also: Local, NodeLocal

virtual RDenseMatrix Element::GlobalShapeD	(	const NodeList &	nlist,
		const Point &	glob
	)		const

inlinevirtual

Returns the values of the shape function derivatives at a global point.

Parameters

glob	global point coordinates

Returns: Matrix (size nNode x Dimension) of shape function derivatives 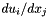at the point for all shape functions associated with the element.

See Also: LocalShapeF, GlobalShapeF, GlobalShapeD

Reimplemented in Triangle3, Triangle3D6, Line2D2, Triangle3D3, Tetrahedron4, Triangle3old, Voxel8, Triangle6, Voxel27, Pixel4, and Tetrahedron10.

Referenced by Pixel4::GlobalShapeD(), and Voxel8::GlobalShapeD().

virtual RVector Element::GlobalShapeF	(	const NodeList &	nlist,
		const Point &	glob
	)		const

inlinevirtual

Returns the values of the shape functions at a global point.

Parameters

nlist	mesh node list
glob	point coordinates in the local element system

Returns: Vector (size nNode) of shape function values at the point for all shape functions associated with the element.

See Also: LocalShapeF, LocalShapeD, GlobalShapeD

Reimplemented in Triangle3, Triangle3D6, Line2D2, Triangle3D3, Tetrahedron4, Triangle3old, Triangle10, Triangle6, Voxel8, Voxel27, Pixel4, and Tetrahedron10.

Referenced by Pixel4::GlobalShapeF(), and Voxel8::GlobalShapeF().

bool Element::HasBoundarySide ( )

inline

Checks if the element contains any surface sides.

Returns: true if the element has at least one boundary side, false otherwise.

Note: The Initialise method must have been executed prior to any calls to HasBoundarySide.

See Also: Initialise, IsBoundarySide

bool Element::HasInterfaceSide ( )

inline

Checks if the element contains any internal interface sides.

Returns: true if the element has at least one internal interface side, false otherwise.

Note: Interfaces define the boundaries between different mesh regions, e.g. for the application of boundary conditions.; The Initialise method must have been executed prior to any calls to HasInterfaceSide.

See Also: Initialise, HasBoundarySide

virtual void Element::Initialise ( const NodeList & nlist )

virtual

Element initialisation.

Calculation of geometric element parameters, including element size and pre-calculation of geometry dependent element matrices.

Parameters

nlist Node list, containing node geometry

Note: Should be called after the node list has been generated, and whenever the node list changes.

Reimplemented in Element_Unstructured, Triangle3, Tetrahedron4, Triangle10, Triangle6, Triangle3D6, Tetrahedron10_ip, Voxel8, Voxel27, Tetrahedron10, Triangle10_ip, Pixel4, Triangle6_ip, Line2D2, Triangle3D3, Quad4, Triangle3old, Wedge6, and Wedge18inf.

virtual double Element::Intd	(	int	i,
		int	k
	)		const

inlinevirtual

Integral of partial shape function derivative over the element.

Parameters

i	node index (range 0 .. nNode-1)
k	coordinate index for the derivative (range 0 .. Dimension-1)

Returns: Value of the integral
$\int_\Omega \frac{\partial u_i(\vec{r})}{\partial x_k} d\vec{r}$

Reimplemented in Tetrahedron4.

virtual RSymMatrix Element::IntDD ( ) const

pure virtual

Integrals of all products of two shape function derivatives over the element.

Returns: Matrix of size nNode x nNode, containing the integrals
$\int_\Omega \nabla u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r}$

See Also: IntDD(int,int)const,
IntF, IntFF, IntFFF, IntFD, IntDD, IntPFF, IntPDD

Implemented in Element_Unstructured, Voxel8, Voxel27, and Pixel4.

virtual double Element::IntDD	(	int	i,
		int	j
	)		const

pure virtual

Integral of a product of two shape function derivatives over the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)

Returns: Value of the integral
$\int_\Omega \nabla u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r}$

See Also: IntDD()const,
IntF, IntFF, IntFFF, IntFD, IntDD, IntPFF, IntPDD

Implemented in Element_Unstructured, Voxel8, Pixel4, and Voxel27.

virtual RSymMatrix Element::Intdd ( ) const

inlinevirtual

Integral of the product of two partial shape function derivatives over the element.

Returns: Matrix of integrals for all element nodes in each dimension.
$\int_\Omega \frac{\partial u_i(\vec{r})}{\partial x_j} \frac{partial u_k(\vec{r})}{\partial x_l} d\vec{r}$
The dimension of the returned matrix is nd x nd, where n is the number of nodes, and d is the dimension of the element (2 or 3). The matrix contains n x n blocks, where each block is of dimension d x d.

Reimplemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Triangle6, Voxel8, Pixel4, and Voxel27.

virtual double Element::IntF ( int i ) const

pure virtual

Integral of a shape function over the element.

Parameters

i	node index (range: 0 .. nNode-1)

Returns: value of the integral
$\int_\Omega u_i(\vec{r}) d\vec{r}$

See Also: IntFF, IntFFF, IntDD, IntFD

Implemented in Triangle3, Line2D2, Tetrahedron4, Triangle3old, Triangle10, Voxel8, Triangle6, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, and Wedge6.

virtual RVector Element::IntFD	(	int	i,
		int	j
	)		const

inlinevirtual

Integral of a product of a shape function and a shape function derivative over the element.

Parameters

i	node index for shape function
j	node index for shape function derivative

Returns: Vector of size Dimension, containing the integral
$\int_\Omega u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r}$

See Also: IntDD, IntFDD, IntPDD

Reimplemented in Triangle3, Line2D2, Triangle3old, and Triangle6.

virtual double Element::IntFd	(	int	i,
		int	j,
		int	k
	)		const

inlinevirtual

Integral of the product of a shape function and a partial shape function derivative over the element.

Parameters

i	node index for shape function (range 0 .. nNode-1)
j	node index for shape function derivative (range 0 .. nNode-1)
k	coordinate index for derivative (range 0 .. Dimension-1)

Returns: Value of the integral
$\int_\Omega u_i(\vec{r}) \frac{\partial u_j(\vec{r})}{\partial x_k} d\vec{r}$

Reimplemented in Triangle3, Line2D2, Voxel8, Triangle6, Pixel4, Tetrahedron4, and Voxel27.

virtual double Element::IntFDD	(	int	i,
		int	j,
		int	k
	)		const

pure virtual

Integral of a product of a shape function and two shape function derivatives over the element.

Parameters

i	node index for shape function
j	first node index for shape function derivative
k	second node index for shape function derivative

Returns: Value of the integral
$\int_\Omega u_i(\vec{r}) \nabla u_j(\vec{r}) \nabla u_k(\vec{r}) d\vec{r}$

See Also: IntDD, IntFD, IntPDD

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Voxel8, Triangle6, Triangle10, Pixel4, Voxel27, Wedge6, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

virtual double Element::IntFdd	(	int	i,
		int	j,
		int	k,
		int	l,
		int	m
	)		const

inlinevirtual

Integral of the product of a shape function and two partial shape function derivatives over the element.

Parameters

i	node index for shape function (range 0 .. nNode-1)
j	node index for shape function derivative (range 0 .. nNode-1)
k	node index for shape function derivative (range 0 .. nNode-1)
l	coordinate index for derivative (range 0 .. Dimension-1)
m	coordinate index for derivative (range 0 .. Dimension-1)

Returns: Value of the integral
$\int_\Omega u_i(\vec{r}) \frac{\partial u_j(\vec{r})}{\partial x_l} \frac{\partial u_k(\vec{r})}{\partial x_m}$

Reimplemented in Triangle3, Line2D2, Voxel8, Tetrahedron4, Pixel4, and Voxel27.

virtual RSymMatrix Element::IntFF ( ) const

pure virtual

Integrals of all products of two shape functions over the element.

Returns: Matrix of size nNode x nNode, containing the integrals
$\int_\Omega u_i(\vec{r}) u_j(\vec{r}) d\vec{r}$

See Also: IntFF(int,int)const, IntF, IntFFF, IntDD, IntFD

Implemented in Triangle3, Line2D2, Tetrahedron4, Triangle3old, Triangle10, Voxel8, Voxel27, Pixel4, Triangle6, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, Wedge6, and Wedge18inf.

virtual double Element::IntFF	(	int	i,
		int	j
	)		const

pure virtual

Integral of a product of two shape functions over the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)

Returns: Value of the integral
$\int_\Omega u_i(\vec{r}) u_j(\vec{r}) d\vec{r}$

See Also: IntFF()const, IntF, IntFFF, IntDD, IntFD

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Triangle10, Triangle6, Voxel8, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, and Wedge6.

virtual double Element::IntFFF	(	int	i,
		int	j,
		int	k
	)		const

pure virtual

Integral of a product of three shape functions over the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)
k	third node index (range 0 .. nNode-1)

Returns: Value of the integral
$\int_\Omega u_i(\vec{r}) u_j(\vec{r}) u_k(\vec{r}) d\vec{r}$

See Also: IntF, IntFF, IntDD, IntFD

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Triangle10, Voxel8, Triangle6, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, and Wedge6.

virtual double Element::IntPd	(	const RVector &	P,
		int	j,
		int	k
	)		const

inlinevirtual

Integral of the product of a nodal function and a partial shape function derivative over the element.

Parameters

P	array of nodal coefficients defining the function
j	node index for shape function derivative (range 0 .. nNode-1)
k	coordinate index for derivative (range 0 .. Dimension-1)

Returns: Value of the integral
$\sum_i P_i \int_\Omega u_i(\vec{r}) \frac{\partial u_j(\vec{r})}{\partial x_k} d\vec{r}$

Reimplemented in Triangle3, Line2D2, Triangle6, and Tetrahedron4.

virtual RSymMatrix Element::IntPDD ( const RVector & P ) const

pure virtual

All integrals of products of a nodal function and two shape function derivatives over the element.

Parameters

P	nodal function coefficients over the mesh

Returns: Matrix of size nNode x nNode, containing the integrals
$\int_\Omega p(\vec{r}) \nabla u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r} = \sum_k p_k \int_\Omega u_k(\vec{r}) \nabla u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r}$

See Also: IntPDD(int,int,const RVector&)const, IntFDD, IntFD, IntPFF

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Voxel8, Pixel4, Triangle6, Wedge6, Triangle10, Voxel27, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

Referenced by Pixel4::IntPDD().

virtual double Element::IntPDD	(	int	i,
		int	j,
		const RVector &	P
	)		const

pure virtual

Integrals of a product of a nodal function and two shape function derivatives over the element.

Parameters

i	first node index
j	second node index
P	nodal function coefficients over the mesh

Returns: Value of the integral
$\int_\Omega p(\vec{r}) \nabla u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r} = \sum_k p_k \int_\Omega u_k(\vec{r}) \nabla u_i(\vec{r}) \nabla u_j(\vec{r}) d\vec{r}$

See Also: IntPDD(const RVector&)const, IntFDD, IntFD, IntPFF

Implemented in Triangle3, Line2D2, Triangle3old, Wedge6, Tetrahedron4, Voxel8, Triangle6, Triangle10, Pixel4, Voxel27, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

virtual RSymMatrix Element::IntPFF ( const RVector & P ) const

pure virtual

Integrals of all products of two shape functions and a nodal function over the element.

Parameters

P	nodal basis coefficients of a function defined over the mesh

Returns: Matrix of size nNode x nNode, containing the integrals
$\int_\Omega p(\vec{r}) u_i(\vec{r}) u_j(\vec{r}) d\vec{r} = \sum_k p_k \int_\Omega u_i(\vec{r}) u_j(\vec{r}) u_k(\vec{r}) d\vec{r}$

See Also: IntPFF(int,int,const RVector&)const,
IntF, IntFF, IntFFF, IntFD, IntDD, IntPDD

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Triangle10, Voxel8, Triangle6, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Wedge6, and Triangle6_ip.

virtual double Element::IntPFF	(	int	i,
		int	j,
		const RVector &	P
	)		const

pure virtual

Integral of a product of two shape functions and a nodal function over the element.

Parameters

i	first node index (range 0 .. nNode-1)
j	second node index (range 0 .. nNode-1)
P	nodal basis coefficients of a function defined over the mesh

Returns: The value of the integral
$\int_\Omega p(\vec{r}) u_i(\vec{r}) u_j(\vec{r}) d\vec{r} = \sum_k p_k \int_\Omega u_i(\vec{r}) u_j(\vec{r}) u_k(\vec{r}) d\vec{r}$

See Also: IntPFF(const RVector&)const,
IntF, IntFF, IntFFF, IntFD, IntDD, IntPDD

Implemented in Triangle3, Line2D2, Triangle3old, Tetrahedron4, Triangle10, Triangle6, Voxel8, Voxel27, Pixel4, Wedge6, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, and Triangle6_ip.

bool Element::IsBoundarySide ( int side )

inline

Checks if a side is on the mesh surface.

Parameters

side	side index (>= 0)

Returns: true if the specified side is a boundary side, false otherwise.

Note: The Initialise method must have been executed prior to any calls to IsBoundarySide.

See Also: Initialise, HasBoundarySide

virtual bool Element::IsNode ( int node )

virtual

Checks if a node is part of the element.

Parameters

node	absolute node index (>= 0)

Returns: true if node appears in the element's node index list, false otherwise.

int Element::IsSide	(	int	nn,
		int *	nd
	)

Checks if a face defined by vertex nodes is part of the element.

Parameters

nn	number of node indices in the supplied array
nd	array of absolute node indices of length nn

Returns: If all node indices in nd are part of the element, and are associated with a single one of the element's sides, the relative side index (>= 0) is returned. Otherwise, -1 is returned.

virtual bool Element::IsSideNode	(	int	side,
		int	node
	)

virtual

Checks if a node is associated with a specific side.

Parameters

side	side index (>= 0)
node	relative node index (>= 0)

Returns: true if node belongs to side, false otherwise.

Note: side must be in the range 0 .. nSide()-1; node must be in the range 0 .. nNode()-1

See Also: nSide, nNode

virtual bool Element::LContains	(	const Point &	loc,
		bool	pad = `true`
	)		const

pure virtual

Checks if a local point coordinate is inside the element.

Parameters

loc	point in local coordinates
pad	Apply padding to the element to ensure that boundary points are considered inside.

Returns: true if the point is inside the element, false otherwise.

Note: If pad == false, then the status of points exactly on the element boundary is undefined. They may or may not be considered inside. Use pad = true to ensure that they are regarded as inside.

See Also: GContains

Implemented in Triangle3, Line2D2, Tetrahedron4, Triangle10, Triangle6, Triangle3old, Voxel8, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, Quad4, and Wedge6.

virtual const RVector& Element::LNormal ( int side ) const

pure virtual

Returns a side normal in local coordinates.

Parameters

side	side index (>= 0)

Returns: Normal to side in local element coordinates.

See Also: DirectionCosine

Implemented in Triangle3, Line2D2, Tetrahedron4, Triangle10, Triangle6, Triangle3old, Voxel8, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, and Wedge6.

Referenced by Pixel4::DirectionCosine(), and Voxel8::DirectionCosine().

virtual Point Element::Local	(	const NodeList &	nlist,
		const Point &	glob
	)		const

pure virtual

Maps a point from global to local element coordinates.

Parameters

nlist	mesh node list
glob	global point coordinates

Returns: Point coordinates in the element's local reference system.

Note: Point glob should have dimension Dimension(); glob does not have to be located inside the element.

See Also: NodeLocal, Global

Implemented in Triangle3, Tetrahedron4, Triangle3D6, Triangle10, Triangle6, Line2D2, Triangle3D3, Voxel8, Tetrahedron10_ip, Voxel27, Pixel4, Tetrahedron10, Triangle10_ip, Triangle3old, Triangle6_ip, Quad4, and Wedge6.

Referenced by Pixel4::Local(), and Voxel8::Local().

virtual RDenseMatrix Element::LocalShapeD ( const Point & loc ) const

pure virtual

Returns the values of the shape function derivatives at a local point.

Parameters

loc	point coordinates in the local element system

Returns: Matrix (size nNode x Dimension) of shape function derivatives 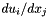at the point for all shape functions associated with the element.

See Also: LocalShapeF, GlobalShapeF, GlobalShapeD

Implemented in Triangle3, Line2D2, Tetrahedron4, Triangle10, Triangle3old, Triangle6, Voxel8, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, Quad4, and Wedge6.

virtual RVector Element::LocalShapeF ( const Point & loc ) const

pure virtual

Returns the values of the shape functions at a local point.

Parameters

loc	point coordinates in the local element system

Returns: Vector (size nNode) of shape function values at the point for all shape functions associated with the element.

See Also: GlobalShapeF, LocalShapeD, GlobalShapeD

Implemented in Triangle3, Line2D2, Tetrahedron4, Triangle10, Triangle3old, Triangle6, Voxel8, Voxel27, Pixel4, Tetrahedron10, Tetrahedron10_ip, Triangle10_ip, Triangle6_ip, Quad4, and Wedge6.

virtual void Element::MapToSide	(	int	side,
		Point &	loc
	)		const

virtual

Translates a point to an element surface.

Parameters

[in]	side	side index (>= 0)
[in,out]	loc	point to be transformed.

Note: Moves loc onto side side by translating it along the side normal.

Reimplemented in Tetrahedron4.

virtual int Element::nNode ( ) const

pure virtual

Returns the number of nodes associated with the element.

Returns: Number of nodes

Implemented in Triangle3, Tetrahedron4, Triangle10, Triangle6, Voxel8, Tetrahedron10_ip, Line2D2, Tetrahedron10, Voxel27, Pixel4, Triangle10_ip, Triangle6_ip, Triangle3old, Quad4, Wedge6, and Wedge18inf.

virtual Point Element::NodeLocal ( int node ) const

pure virtual

Returns the local coordinates of an element node.

Parameters

node	node index (>= 0)

Returns: Node coordinates in the element's local reference system.

See Also: Local, Global

Implemented in Triangle3, Tetrahedron4, Triangle10, Line2D2, Triangle6, Voxel8, Voxel27, Pixel4, Tetrahedron10_ip, Tetrahedron10, Triangle3old, Triangle10_ip, Triangle6_ip, Quad4, and Wedge6.

virtual int Element::nSide ( ) const

pure virtual

Returns the number of element sides.

Returns: Number of sides

Note: For 3-D elements, this returns the number of element faces (4 for tetrahedra, 6, for voxels, etc). For 2-D elements, it returns the number of boundary segments (3 for triangles, 4 for pixels, etc.)

Implemented in Triangle3, Tetrahedron4, Triangle10, Triangle6, Line2D2, Voxel8, Tetrahedron10_ip, Tetrahedron10, Voxel27, Pixel4, Triangle10_ip, Triangle6_ip, Triangle3old, Quad4, and Wedge6.

virtual int Element::nSideNode ( int side ) const

pure virtual

Returns the number of vertices associated with a side.

Parameters

side	side index (>= 0)

Returns: Number of vertices connected to the side.

See Also: nSide, nNode, nSideNode

Implemented in Triangle3, Tetrahedron4, Triangle10, Triangle6, Line2D2, Voxel8, Tetrahedron10_ip, Tetrahedron10, Voxel27, Pixel4, Triangle10_ip, Triangle6_ip, Triangle3old, Quad4, and Wedge6.

void Element::operator= ( const Element & el )

Element assignment.

Parameters

el	right-hand side element operand

Note: Allows operations of the form
el1 = el2;; This operation is only allowed if both elements are of the same type (e.g. 4-noded tetrahedra, etc.) It is not possible to change the type of an element.; This operation copies the node indices from el to *this.

virtual void Element::PostInitialisation ( const NodeList & nlist )

inlinevirtual

Element setup after mesh initialisation.

This method is called after all mesh elements have been initialised. It can be used to perform any element initialisation steps that require the rest of the mesh to be initialised.

Reimplemented in Element_Unstructured, and Voxel8.

virtual int Element::QuadRule	(	int	order,
		const double **	wght,
		const Point **	absc
	)		const

inlinevirtual

Returns the weights and abscissae of quadrature rules over the element.

Parameters

order	quadrature order (>= 1)
wght	pointer to an array of quadrature weights
absc	pointer to an array of quadrature abscissae

Returns: Number of quadrature points

Note

The required order of a quadrature rule depends on the type of integral to be performed. Examples:

IntF: order = 1
IntFF, IntD: order = 2
intFFF, IntFD: order = 3
IntDD: order = 4 etc.

Reimplemented in Triangle3, and Triangle3old.

virtual Point Element::SideCentre ( int side ) const

virtual

Returns the centre point of a side.

Parameters

side	side index (>= 0)

Returns: side centre, defined as the barycentre of the associated nodes.

Element* Element::SideNeighbour ( int side ) const

returns a pointer to the element connected at 'side', or NULL if this is a boundary side.

Parameters

side	side index (>= 0)

Returns: Element pointer or NULL

Note: This function is only supported if Mesh::PopulateNeighbourLists has been called before.

int Element::SideNeighbourIndex ( int side ) const

Returns the list index of the element connected at 'side', or -1 if this is a boundary side.

Parameters

side	side index (>= 0)

Returns: Element list index (>- 0) or -1

Note: This function is only supported if Mesh::PopulateNeighbourLists has been called before.

virtual int Element::SideNode	(	int	side,
		int	node
	)		const

pure virtual

Returns relative node index for a side vertex.

Parameters

side	side index (>= 0)
node	side node index (>= 0)

Returns: Relative node index

Note: Returns the node index for one of the vertices of a side.; side must be in the range 0 .. nSide()-1; node must be in the range 0 .. nSideNode (side); The return value is in the range 0 .. nNode()-1

See Also: nNode, nSide, nSideNode

Implemented in Triangle3, Tetrahedron4, Triangle10, Triangle6, Line2D2, Voxel8, Tetrahedron10_ip, Tetrahedron10, Voxel27, Pixel4, Triangle10_ip, Triangle6_ip, Triangle3old, Quad4, and Wedge6.

virtual double Element::SideSize	(	int	side,
		const NodeList &	nlist
	)		const

inlinevirtual

Returns the size of an element side.

Parameters

side	side index (>= 0)
nlist	mesh node list

Returns: Size of the element face (length for 2-D elements, area for 3-D elements).

See Also: Size

Reimplemented in Triangle3, Tetrahedron4, Line2D2, Tetrahedron10, and Triangle3old.

virtual double Element::Size ( ) const

pure virtual

Returns the element size.

Returns: Area (for 2-D elements) or volume (for 3-D elements) of the element.

See Also: SideSize

Implemented in Element_Unstructured, Voxel8, Voxel27, and Pixel4.

int Element::SubdivisionLevel ( ) const

Returns the element's subdivison level.

Returns: subdivision level (>= 0)

Note: By default, all elements have level 0. The subdivision level can increase during dynamic mesh refinement.

virtual Point Element::SurfToLocal	(	int	side,
		const Point &	p
	)		const

inlinevirtual

Maps a point from surface coordinates to local element coordinates.

Parameters

side	side index (>= 0)
p	surface point coordinates.

Returns: Point coordinates in the element's local reference system.

Note: Surface point p should have dimension Dimension()-1

See Also: Local, NodeLocal

Reimplemented in Triangle3, Line2D2, Triangle3D6, Tetrahedron4, Triangle3D3, Triangle3old, and Tetrahedron10.

virtual BYTE Element::Type ( ) const

pure virtual

Returns an element type identifier.

Returns: Element type identifier (see Element type identifiers).

Implemented in Triangle3, Tetrahedron4, Triangle10, Triangle6, Triangle3D6, Voxel8, Tetrahedron10_ip, Voxel27, Tetrahedron10, Triangle10_ip, Pixel4, Triangle6_ip, Line2D2, Triangle3D3, Quad4, Triangle3old, Wedge6, and Wedge18inf.

The documentation for this class was generated from the following file:

/home/ucacmas/src/toast/toast_sf/toastpp-code/toast/trunk/src/libfe/element.h

Public Member Functions

Public Attributes

Protected Attributes

Friends

Detailed Description

Member Function Documentation