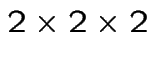Example: One bit AND, NAND, OR and NOR

Each function has two 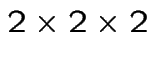$2\times 2\times2$ transition matrices

Each function is symmetric, so its two matrices identical

Each function has opposite (e.g. AND and NAND)

So mean matrix has the same value at every element

$$N=1/4 \begin{array}{cc} \begin{array}{cc} 1 & 1 \\ 1 & 1 \\ ... ...begin{array}{cc} 1 & 1 \\ 1 & 1 \\ \end{array}% \end{array}%$$

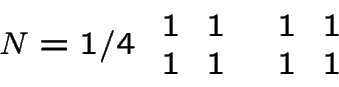
M₁ is independent of u₀

M₁ is irreducible, doubly stochastic, with non-zero diagonal

Output of random function independent of inputs and random

Since the coefficients p' sum to 1, this is true for every M_i.

Output of whole tree random regardless of size