I.e.
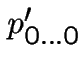 tends to 0.5 as we get further from the leaf,
tends to 0.5 as we get further from the leaf,
i.e. as i increases, so Mi is dominated by the first few terms.
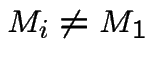 ,
,
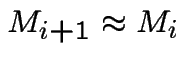 and so the current value
along the longest path will become Markovian.
and so the current value
along the longest path will become Markovian.
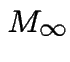 we can calculate the probability distribution of the output of large
random trees
and how big the threshold size is.
we can calculate the probability distribution of the output of large
random trees
and how big the threshold size is.
Note that unlike linear programs, these may depend upon the programs inputs.