How Well Does Genetic Programming Generalise? ¹

W.B. Langdon and J.P. Nordin

Centrum voor Wiskunde en Informatica, Kruislaan 413, NL-1098 SJ, Amsterdam

Chalmers University of Technology, S-41296, Göteborg, Sweden nordin@fy.chalmers.se

Introduction

We want to find patterns in data.
Want generalisation on unseen data.
To find the ``essence'' of the data.

We turn genetic programming (GP) on its head.
Instead of GP matching training data.
We construct a function to match training data.
Seed GP with it.

Can GP evolve the function to be more general?

Test problems

• Programmatic image compression problem

• North American Pima Indians diabetes

• Wisconsin Breast Cancer Database

• Real-world customer profiling problem with
  [4]85 attributes (Benelearn'99 and COIL'2000).

Programmatic Compression

Target image (256 by 167). Note variety of repeating patterns.

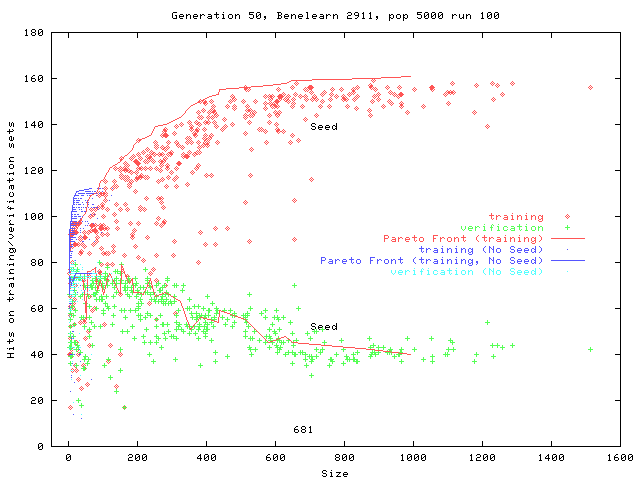
Pima Diabetes

Exactly matches training data $\Rightarrow$ General solution

Very simple program is as good as ML

Objective:	Find a program that predicts Diabetes.
Terminal set:	One terminal per data attribute (8). For each attribute, create unique random constants between its minimum and maximum value (in the training set). Use integers where the attribute has integer only values (total 255 primitives).
Function set:	IF IFLTE MUL ADD DIV SUB AND OR NAND NOR XOR EQ APPROX NOT
Fitness cases:	Training 576 (194 positive). 192 (74 positive) for verification only.
Fitness:	number correct (hits).
Selection:	2 objectives, hits and size, combined in Pareto tournament group size 7. Non-elitist, generational. Fitness sharing (comparison set 81)
Wrapper:	Value $\ge 0.5$ taken as true
Pop Size:	500
Max prog. size:	no limit
Initial pop:	100% seeded or created using ``ramped half-and-half'' (no duplicate checking).
Parameters:	90% one child crossover, 2.5% function point mutation (rate 100/1024), 2.5% constant mutation (rate 100/1024), 2.5% shrink mutation, 2.5% size fair mutation (subtree size$\le$30)
Termination:	Maximum number of generations G = 50

Seed size	Highest Verification			First program $\ge 137$
	Hits	Size	Gen	Size	Gen	% runs $\ge 137$
none (Pareto)	121	25	8			0
none (scalar)	131	31	10	5	17	40
20	143	34	35	3	26	100
288	144	1603	40	4	22	100
576	142	6369	41	62	33	100

Evolution of Pareto front in seeded (288) Pima run

Wisconsin Breast Cancer

 

Objective:	Find a program that predicts Breast Cancer.
Terminal set:	One terminal per data attribute (9). Constants -1 to 10
Fitness cases:	351 (130 positive). 348 (111 positive) verification tests.

Cancer. Highest verification score on Pareto front
Seed size	Highest Verification			First program $\ge 326$
	Hits	Size	Gen	Size	Gen	% runs $\ge 326$
none (Pareto)	333	23	28	6	14	100
20	330	101	34	65	32	100
128	327	46	39	42	38	80
351	327	6422	42	2622	47	80

Insurance Customer Profiling

 

Given 85 attributes relating to a customer, such as age, number of children, number of cars, income, other insurance policies they hold, predict if they want caravan insurance.

GP generalises the C4.5 seed. However over training increases with size of programs.

Conclusions

• It is possible to start GP with perfect individuals and find good generalisers.

• Sometimes the seed can be created from a very small sample of the training data.

• Offers easy way to hybridise GP with other techniques.

• Shows the often assumed relationship between long programs and poor generalisation.

• It might seem a bit provocative to have a perfect individual from the start, but the approach turns out to be feasible. We think that this is because GP has a built in ability to generalise.