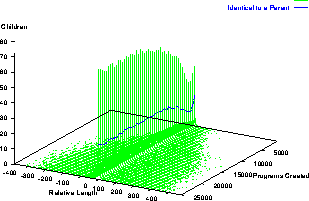
Figure 10: Change in length of offspring relative to first parent where score is the same. Normal runs, means of 50 runs.
In Section 2 we argued that there are more long programs with a given performance than short ones and so a random search for programs with a given level of performance is more likely to find long programs. We would expect generally (and it has been reported on a number of problems) that crossover produces progressively fewer improved solutions as evolution proceeds and instead in many problems selection drives it to concentrate upon finding solutions with the same fitness. Apart from the minimum and maximum size restrictions crossover is random so we would expect to see it finding more long solutions than short ones. The change in program length of programs produced by crossover which have the same fitness as their first parent is plotted in Figure 10. At first sight Figure 10 is disappointingly symmetric with a large central spike of programs with the same length and rapidly falling tails either side of zero. Initially 8% of crossovers produce a child which has the same length and fitness as its first parent. This proportion falls to a minimum of 6% in generation 4 and then rises progressively to 15% at the end of the run.
The dashed line on Figure 10 plots the number of children in each generation produced by crossovers that are identical to one or other of their parents. On the ant problem 5% of crossovers produce such clones.

Figure 10:
Change in length of offspring relative to first parent
where score is the same.
Normal runs,
means of 50 runs.
Closer examination of the data in Figure 10 reveals that on average (cf. Figure 11) there is a bias towards longer programs. On average programs with the same fitness as their first parent are always longer than it. From generation 4 to 23 they are on average about 3 program nodes longer. Presumably due to the average program length approaching the upper limit, the bias falls to about 1 after generation 33 but remains positive.
Part of the reason for the central peak of Figure 10 is a result of another aspect of GP crossover: almost all the genetic material is inherited from the first parent. Crossover points are typically drawn from close to the leafs of both parents simply because for large bushy trees most parts of a tree are close to its leafs. While the expected size of crossover fragments depends in detail upon the trees selected as parents and the relative weighting applied to functions and terminals, cf. Table 1, typically both the inserted subtree and the subtree it replaces consist of a function and its leafs. Since these subtrees are short together they produce a small change in total size. It seems likely that small changes are less likely to effect fitness than big ones, hence the spike in Figure 10. Inheriting principally from one parent is in sharp contrast to more traditional GAs (and indeed sexual reproduction in ``higher organisms'' in nature) where offspring receive about the same amount of genetic material from each parent.
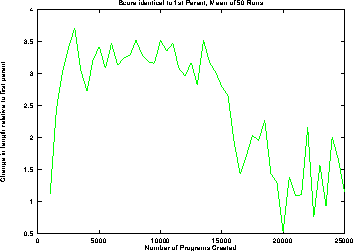
Figure 11:
Mean change in length of offspring relative to first parent
where score is the same.
Normal runs,
means of 50 runs.
Every program terminal uses one energy unit each time it is executed. Thus the amount of energy used when executing a program gives the actual number of terminals it has used. From Figure 12 we see typically only 5--10 terminals are used per execution (a move and four turns allows the ant to move forward whilst searching either side of it), While different parts of the program could be executed each time it is called, in the cases of those that have been analysed in detail, mostly code that has been used before is re-executed. That is large programs evolve which contain small functional parts.
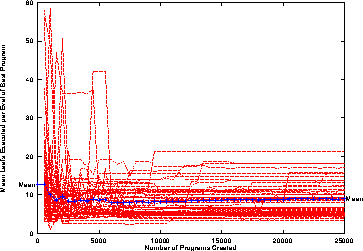
Figure 12:
Energy used per call of ``best'' program.
50 normal runs.