


Next: Plagiarism Penalty
Up: Fitness Functions
Previous: Santa Fe trail
In the second set of experiments the fixed Santa Fe trail is replaced
by 50 randomly generated trails each containing 80 food items.
Each generation is tested on a different trail,
however the order of the trails is the same in each run.
(The test case is available via
anonymous ftp node ftp.cs.bham.ac.uk
directory pub/authors/W.B.Langdon/gp-code
in file dynamic.trl revision 1.11).
Each trail is created by appending (in randomly chosen orientations) 20
randomly chosen trail fragments each containing 4 food pellets.
We use the 17 fragments shown in Fig. 1.
A uniform choice from these 17 fragments appeared to produced trails
which were too difficult.
Therefore, like the Santa Fe trail, the randomly produced trails were
made easier at the start. This was implemented by increasing the
chance of selecting the lower numbered fragments (as they have smaller
gaps in the trail).
In detail, start at the origin facing along the x-axis with n=0.
Select a trail fragment
uniformly from fragments numbered 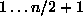 when n is less than 9 and
uniformly from the whole set when it is bigger.
The chosen fragment is then rotated and/or reflected into a random
orientation from those available (see Fig. 1).
However the transformation must be compatible with the current direction.
The fragment is then appended to the trail,
possibly changing the current direction
and n is incremented.
Unless there already 20 fragments in the trail,
go back and select another fragment.
Once the trail is complete,
it is checked to see it does not cross the start position and does not
fold back over itself
(i.e. food pellets are not closer than 2 grid squares, unless they are
on the same part of the trail).
If either check fails,
the trail is discarded and a new one is created.
when n is less than 9 and
uniformly from the whole set when it is bigger.
The chosen fragment is then rotated and/or reflected into a random
orientation from those available (see Fig. 1).
However the transformation must be compatible with the current direction.
The fragment is then appended to the trail,
possibly changing the current direction
and n is incremented.
Unless there already 20 fragments in the trail,
go back and select another fragment.
Once the trail is complete,
it is checked to see it does not cross the start position and does not
fold back over itself
(i.e. food pellets are not closer than 2 grid squares, unless they are
on the same part of the trail).
If either check fails,
the trail is discarded and a new one is created.
In practice it is difficult to create a contiguous winding trail of 80
food pellets in a 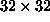 grid without it overlapping
itself. Therefore a toroidal grid of
grid without it overlapping
itself. Therefore a toroidal grid of 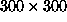 was used.
The time available to the ant to transverse each trail is calculated
as it is created.
The time allowed is five
plus the sum of the time allocated to each of the fragments it
contains (see Fig. 1)
plus a further five for each occasion when fragments at
different orientations are used (i.e. where a new bend is introduced).
In practice this makes the problem very difficult.
In several runs the best programs evolved showed true trail following
abilities but were marginally too inefficient to follow all the trails
completely within the time limit.
was used.
The time available to the ant to transverse each trail is calculated
as it is created.
The time allowed is five
plus the sum of the time allocated to each of the fragments it
contains (see Fig. 1)
plus a further five for each occasion when fragments at
different orientations are used (i.e. where a new bend is introduced).
In practice this makes the problem very difficult.
In several runs the best programs evolved showed true trail following
abilities but were marginally too inefficient to follow all the trails
completely within the time limit.
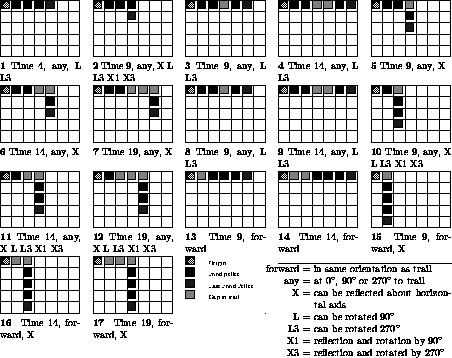
Figure 1:
Fragments of Santa Fe trail used to form random trails.



Next: Plagiarism Penalty
Up: Fitness Functions
Previous: Santa Fe trail
William B Langdon
Mon Dec 8 19:56:15 GMT 1997
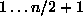 when n is less than 9 and
uniformly from the whole set when it is bigger.
The chosen fragment is then rotated and/or reflected into a random
orientation from those available (see Fig. 1).
However the transformation must be compatible with the current direction.
The fragment is then appended to the trail,
possibly changing the current direction
and n is incremented.
Unless there already 20 fragments in the trail,
go back and select another fragment.
Once the trail is complete,
it is checked to see it does not cross the start position and does not
fold back over itself
(i.e. food pellets are not closer than 2 grid squares, unless they are
on the same part of the trail).
If either check fails,
the trail is discarded and a new one is created.
when n is less than 9 and
uniformly from the whole set when it is bigger.
The chosen fragment is then rotated and/or reflected into a random
orientation from those available (see Fig. 1).
However the transformation must be compatible with the current direction.
The fragment is then appended to the trail,
possibly changing the current direction
and n is incremented.
Unless there already 20 fragments in the trail,
go back and select another fragment.
Once the trail is complete,
it is checked to see it does not cross the start position and does not
fold back over itself
(i.e. food pellets are not closer than 2 grid squares, unless they are
on the same part of the trail).
If either check fails,
the trail is discarded and a new one is created.
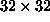 grid without it overlapping
itself. Therefore a toroidal grid of
grid without it overlapping
itself. Therefore a toroidal grid of 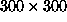 was used.
The time available to the ant to transverse each trail is calculated
as it is created.
The time allowed is five
plus the sum of the time allocated to each of the fragments it
contains (see Fig.
was used.
The time available to the ant to transverse each trail is calculated
as it is created.
The time allowed is five
plus the sum of the time allocated to each of the fragments it
contains (see Fig. 