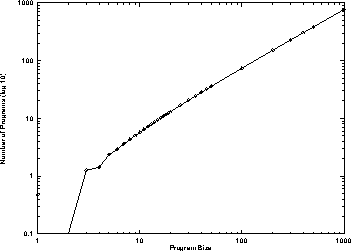
Figure 1: Number of programs of a specific length (note log log scale)
Why Ants are
Previous: The Artificial Ant
The number of different programs of a specific length is given by the size of the terminal set and the numbers of different functions in the function set of each arity (branching factor). To create a tree of a specific length a corresponding number of functions of each branching factor and number of leafs must be used. Where there are more than one branching factor available in the function set, there may be multiple combinations of function arity which give rise to a tree of the required size. In general there are multiple ways of arranging the branches and leafs. Each way gives rise to a distinct tree shape. Finally, where there are more than one terminal or more than one function of a given arity, there are multiple programs of the same shape. The number of different programs in the ant problem is plotted against their lengths in Figure 1 (and is tabulated in the ``Total'' row at the bottom of Table 2). As expected the number of programs grows approximately exponentially with the length of the programs. (The program used to calculate the number of programs is available via anonymous ftp from ftp.cs.bham.ac.uk in pub/authors/W.B.Langdon/gp-code/ntrees.cc).
For the shorter programs it is feasible to explore the program space exhaustively. Table 2 summarises the programs space up to programs of length 14. Table 2 shows the program space is highly asymmetric with almost all programs having very low scores and the proportion with higher scores falling rapidly (but not monotonically) to a low point near 72. Above 72 it rises slightly. The modal score is zero, the median is one and the mean rises with length from 1 to 2.7 while the standard deviation remains near 4 (cf. Figure 7). There is some dependence upon program length and, as expected, programs must be above a minimum size to reach modest scores. However above the minimum size the number of programs with a given score rises rapidly, being a roughly constant proportion of the total number of programs. There are an unexpectedly high number of solutions (albeit a tiny fraction of the total) and their number similarly grows with program size.
For longer programs exhaustive search is not feasible and instead we sampled the program space randomly in a series of Monte Carlo trials for a number of program sizes. For each such size between 10,000,000 random programs where generated and tested. The random programs where chosen uniformly from the set of possible programs of the specific length using the bijective random tree creation algorithm described in [Alonso and Schott1995, Chapter 4,].
Where there are multiple different combinations of function arity which give rise to trees of the required size, one was chosen at random in proportion to the number of trees it contains. Each tree was converted to a program by labelling each of its nodes with a function or terminal of the correct arity chosen uniformly at random from those that match in the function or terminal set. In this way we ensure every program of the specified length has the same chance of being chosen.

Figure 1:
Number of programs of a specific length (note log log scale)
| Length | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Score | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 0 | 2 | 0 | 12 | 16 | 136 | 423 | 2262 | 10452 | 49088 | 252803 | 1227679 | 6443754 | 32595908 | 171997308 |
| 1 | 0 | 0 | 2 | 4 | 18 | 150 | 449 | 3058 | 13806 | 77269 | 380979 | 2070276 | 10954364 | 58002558 |
| 2 | 0 | 0 | 0 | 1 | 3 | 25 | 112 | 909 | 3429 | 21902 | 123174 | 646831 | 3587432 | 19987018 |
| 3 | 1 | 0 | 2 | 6 | 31 | 96 | 530 | 2779 | 11736 | 63996 | 318817 | 1656409 | 8501211 | 45339974 |
| 4 | 0 | 0 | 0 | 0 | 3 | 14 | 72 | 527 | 2526 | 16250 | 86999 | 501521 | 2820383 | 15927690 |
| 5 | 0 | 0 | 0 | 0 | 2 | 10 | 58 | 417 | 1844 | 13047 | 67895 | 390963 | 2213475 | 12466189 |
| 6 | 0 | 0 | 0 | 0 | 1 | 8 | 25 | 177 | 1155 | 6826 | 33174 | 216479 | 1248818 | 6766377 |
| 7 | 0 | 0 | 0 | 0 | 2 | 13 | 35 | 266 | 1601 | 8076 | 39428 | 240187 | 1324912 | 6872615 |
| 8 | 0 | 0 | 0 | 0 | 3 | 10 | 68 | 412 | 1818 | 10785 | 56857 | 303276 | 1580134 | 8846059 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 28 | 183 | 1392 | 8218 | 57485 | 348331 | 2053040 |
| 10 | 0 | 0 | 0 | 0 | 1 | 2 | 18 | 76 | 461 | 2758 | 12465 | 75079 | 406998 | 2276683 |
| 11 | 0 | 0 | 2 | 0 | 16 | 51 | 297 | 907 | 5876 | 27403 | 120960 | 659392 | 3245735 | 16642082 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 52 | 190 | 1326 | 8296 | 45293 | 258390 | 1525769 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 40 | 154 | 1203 | 8011 | 44681 | 266859 | 1548594 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 24 | 105 | 770 | 5437 | 27113 | 169161 | 1041738 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 75 | 150 | 1313 | 11513 | 41711 | 226363 | 1528861 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 34 | 350 | 2584 | 15053 | 104018 | 654943 |
| 17 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | 35 | 167 | 1108 | 4962 | 33175 | 197400 | 1078896 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 13 | 190 | 1764 | 11192 | 83119 | 570147 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 66 | 593 | 3028 | 18180 | 101133 | 660977 |
| 20 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | 20 | 105 | 763 | 3985 | 25601 | 179522 | 938185 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 13 | 56 | 448 | 2501 | 16089 | 107227 | 581413 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | 71 | 639 | 2825 | 21205 | 129354 | 692285 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 47 | 489 | 2372 | 15321 | 83764 | 509240 |
| 24 | 0 | 0 | 0 | 0 | 0 | 4 | 12 | 47 | 293 | 1723 | 6688 | 39676 | 194484 | 1048249 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 36 | 315 | 1586 | 10698 | 65746 | 359170 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 23 | 240 | 1785 | 11356 | 76602 | 379975 |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 16 | 222 | 1262 | 8820 | 54491 | 306671 |
| 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 18 | 153 | 1049 | 7208 | 51024 | 258757 |
| 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 118 | 605 | 4705 | 30333 | 184386 |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 23 | 203 | 922 | 6483 | 40544 | 215169 |
| 31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 120 | 624 | 5167 | 37145 | 191740 |
| 32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 48 | 387 | 2859 | 21765 | 129411 |
| 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 13 | 132 | 898 | 5315 | 31898 | 158423 |
| 34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 12 | 99 | 519 | 3648 | 23694 | 125950 |
| 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 5 | 50 | 298 | 2490 | 20548 | 105190 |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 12 | 106 | 349 | 2905 | 16828 | 98260 |
| 37 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 18 | 104 | 595 | 3189 | 20800 | 99885 |
| 38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 21 | 183 | 637 | 4054 | 17473 | 106100 |
| 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 79 | 226 | 1782 | 8274 | 54753 |
| 40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 79 | 267 | 1888 | 9477 | 56608 |
| 41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 57 | 245 | 1682 | 8812 | 49873 |
| 42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 11 | 92 | 263 | 1821 | 9083 | 51056 |
| 43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 8 | 78 | 190 | 1688 | 7681 | 47354 |
| 44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 109 | 808 | 4988 | 27119 |
| 45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 84 | 756 | 3929 | 24649 |
| 46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 53 | 184 | 1165 | 5234 | 30441 |
| 47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 5 | 42 | 133 | 1068 | 6063 | 30738 |
| 48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 14 | 62 | 532 | 2978 | 16510 |
| 49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 30 | 293 | 1917 | 11133 |
| 50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 41 | 142 | 970 | 3467 | 20849 |
| 51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 38 | 122 | 748 | 2731 | 16387 |
| 52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 10 | 160 | 774 | 6193 |
| 53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 22 | 307 | 1287 | 8526 |
| 54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 26 | 128 | 1568 |
| 55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 6 | 105 | 340 | 3437 |
| 56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 73 | 289 | 2082 |
| 57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 58 | 617 | 2212 |
| 58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 24 | 146 | 949 |
| 59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 316 |
| 60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 46 | 229 | 1790 |
| 61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 30 | 223 | 1435 |
| 62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 29 | 1113 |
| 63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 85 | 285 | 4538 |
| 64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 23 | 337 |
| 65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 53 | 1610 |
| 66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 66 |
| 67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 31 | 435 |
| 68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 90 |
| 69 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | 2394 |
| 70 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1063 |
| 71 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2344 |
| 72 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 18 |
| 73 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 525 |
| 74 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 42 | 119 | 868 |
| 75 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 146 |
| 76 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 174 |
| 77 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 26 | 113 | 733 |
| 78 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 34 | 158 | 991 |
| 79 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 16 | 137 | 755 |
| 80 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 104 | 499 | 3530 |
| 81 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 64 | 157 | 2126 |
| 82 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 10 | 60 | 363 |
| 83 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 60 | 76 | 1367 |
| 84 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21 | 188 | 747 | 5559 |
| 85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 223 | 459 | 5734 |
| 86 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 110 | 173 | 3103 |
| 87 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 27 | 194 | 563 | 3420 |
| 88 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 57 | 399 | 1188 | 6951 |
| 89 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 48 | 470 | 2676 |
| Total | 3 | 0 | 18 | 27 | 216 | 810 | 3969 | 20412 | 95256 | 516132 | 2554416 | 13712490 | 71521461 | 382794984 |
| Mean | 1 | 0 | 1.7 | 0.9 | 1.7 | 1.9 | 2.0 | 2.06903 | 2.24659 | 2.42444 | 2.44969 | 2.59006 | 2.70357 | 2.76907 |
| SD | 3.7 | 0 | 4.4 | 3.8 | 4.4 | 4.4 | 4.4 | 4.45867 | 4.57353 | 4.79021 | 4.76974 | 4.94338 | 4.98586 | 5.04057 |
| Max | 3 | 0 | 11 | 3 | 11 | 24 | 37 | 47 | 51 | 55 | 89 | 89 | 89 | 89 |

Figure 2:
Proportion of programs of a given length by their fitness.
Values for lengths 15 and above are based on Monte Carlo sampling.
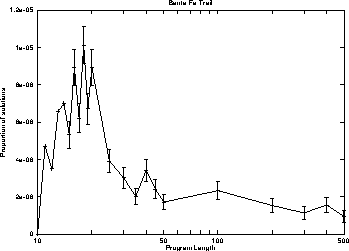
Figure 3:
Proportion of programs of a given length which are solutions.
Error bars indicate standard error on Monte Carlo estimates.
Figure 2 shows that the proportion of programs with a given score is approximately constant for a wide range of program lengths. Since the total number of programs rises rapidly, this means the number of programs with a given score also rises rapidly with length. This confirms assumptions in [Langdon and Poli1997a].
With any Monte Carlo technique there will be some stochastic error in the estimates. In the case of rare events (such as finding a solution to the ant problem) this could be large. The stochastic error was kept reasonable by using a large number of trials so a modest number of solutions were found at each length (between 9 and 101 and on average 39).
An estimate of the stochastic error is plotted in Figure 3 using error bars.
Why Ants are
Previous: The Artificial Ant