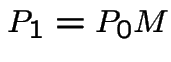 ,
,
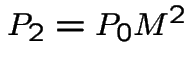 ,
,
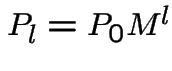
Eigenvectors ![]() of matrix
of matrix ![]() satisfy
satisfy ![]() ,
where
,
where
![]() is the eigenvalue associated with eigenvalue
is the eigenvalue associated with eigenvalue ![]() .
I.e.
.
I.e. ![]() is parallel to
is parallel to ![]() .
.
Repeated multiplication of ![]() by
by ![]() will cause it to shrink
exponentially.
will cause it to shrink
exponentially.
![]() ,
,
![]() ,
,
![]() .
.
![]() can be written as linear sum of its components (
can be written as linear sum of its components (![]() ) parallel to the
eigenvectors.
I.e.
) parallel to the
eigenvectors.
I.e.
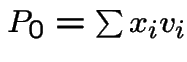
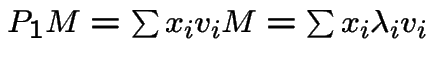
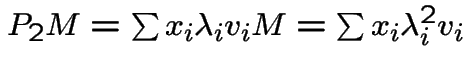
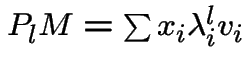
Repeated multiplication of ![]() by
by ![]() will shrink components
corresponding to small
will shrink components
corresponding to small ![]() .
I.e. except
.
I.e. except ![]() ,
are transients.
,
are transients.
Eventually only left with component parallel to eigenvector with largest eigen value.