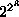 ) three input Boolean functions
however it is not practical to use them to experimentally confirm any
of the NFL theorems.
This is because the number of fitness functions (i.e. problems) is too big.
) three input Boolean functions
however it is not practical to use them to experimentally confirm any
of the NFL theorems.
This is because the number of fitness functions (i.e. problems) is too big.
Roughly speaking NFL says ``the average performance of [search]
algorithms across all possible problems is identical''
[Wolpert and
Macready1997, page 67,].
There are only 256 (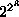 ) three input Boolean functions
however it is not practical to use them to experimentally confirm any
of the NFL theorems.
This is because the number of fitness functions (i.e. problems) is too big.
) three input Boolean functions
however it is not practical to use them to experimentally confirm any
of the NFL theorems.
This is because the number of fitness functions (i.e. problems) is too big.
In GP we consider only a small number of fitness functions, typically only one. The three input boolean functions are unusual in that 256 fitness functions have been investigated. However this is still a miniscule proportion of all the possible fitness functions and so NFL does not apply. Indeed the performance of three search algorithms (GP [Koza1992], hill climbing [Lang1995] and uniform random search) are not identical when averaged across all 256 three input Boolean functions.
Conventionally the fitness of a Boolean function of n inputs
is defined as the number of times its output matches that required
when tested upon all possible combinations of inputs.
The total number of test patterns is 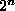 .
Therefore the fitness function yields a value in
.
Therefore the fitness function yields a value in 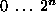 and the total number of possible fitness functions is
and the total number of possible fitness functions is 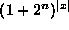 where |x| is the size of the search space.
If we consider searching in the space of trees then |x| is already
very big and so considering all
where |x| is the size of the search space.
If we consider searching in the space of trees then |x| is already
very big and so considering all 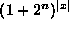 fitness functions is infeasible.
(A program to calculate |x|
fitness functions is infeasible.
(A program to calculate |x|
is available from ftp node ftp.mad-scientist.com directory pub/genetic-programming/code sub-directory gp-code in file ntrees.cc and via my home page).
If instead of considering searching the space of trees,
we consider search in the space of the 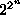 Boolean functions
themselves
then there are only
Boolean functions
themselves
then there are only 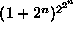 possible fitness
functions.
In the case of n=3 this is
possible fitness
functions.
In the case of n=3 this is 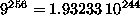 .
Clearly comparing the performance of two or more search algorithms
on this number of problems is still infeasible.
.
Clearly comparing the performance of two or more search algorithms
on this number of problems is still infeasible.
If
we limit ourselves to n=2,
i.e. the 16 (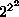 ) Boolean functions of 2 bits,
there are only
) Boolean functions of 2 bits,
there are only 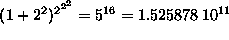 possible
fitness functions.
While it might be feasible to evaluate the performance of various
search algorithms on them and so
experimentally confirm NFL,
such a demonstration is unlikely to be persuasive
due to the small size of the search space.
The small number of points in the search space
makes it likely that stochastic search techniques such as GAs
will resample one or
more points.
NFL explicitly requires the algorithms not to do so.
Any measured difference in performance between algorithms is likely to
be due to this and stochastic noise inherent in randomised search
techniques.
possible
fitness functions.
While it might be feasible to evaluate the performance of various
search algorithms on them and so
experimentally confirm NFL,
such a demonstration is unlikely to be persuasive
due to the small size of the search space.
The small number of points in the search space
makes it likely that stochastic search techniques such as GAs
will resample one or
more points.
NFL explicitly requires the algorithms not to do so.
Any measured difference in performance between algorithms is likely to
be due to this and stochastic noise inherent in randomised search
techniques.