Number of fitness evaluations required

**Table A.1:** Number of trial programs that must be generated to solve problems (with 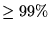$\ge 99\%$ assurance) and the corresponding total number of program executions
Problem Name	Parameters		Effort	Runs/Eval		Executions
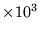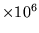	Table	Page	( $\times 10^{3}$ )	Max	Mean	( $\times 10^{6}$ )
Stack	4.2	66	938	160	-	150
Queue: shuffler	5.5	95	383,680	320	-	123,000
Given MInc	5.7	99	3,360	320	320	1,075
Evolving MInc	5.10	108	86,000	320	320	27,520
List	6.3	127	254,000	538	173	44,000
List in two parts	6.3	127	2,580	538	406	1,050
Nested Brackets	7.1	145	190	1,403	1,403	266
Dyck Language
(stack given)	7.3	150	230	1,756	729	167
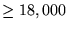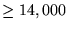(indexed memory)	7.3	150	$\ge 18,000$	1,756	788	$\ge 14,000$
Reverse Polish
(stack given)	7.5	156	2,530	970	900	2,300
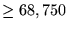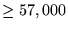(indexed memory)	7.5	156	$\ge 68,750$	970	822	$\ge 57,000$

Table A.1 summarises the estimated effort, in terms of the number of trial solutions evaluated, required to solve (with at least 99% assurance) the problems presented in this book. Where problems were not solved a lower bound has been calculated based on assuming the very next run would have succeeded by generation 25.

The number of program executions required (for 99% probability of solving the problem) is estimated by multiplying the number of trial solutions by the mean number of times each was run during its fitness testing. Where the mean number of program executions per program tested is not available, the maximum is used to give an estimated upper bound. Run time reductions via: ancestor fitness re-use (cf. Section D.5), ADF caching (cf. Section D.6) and avoiding fitness evaluation of individuals produced by reproduction, are excluded.

Appendix A (GP and Data Structures)